
문제
서훈이는 오늘 있었던 알고리즘 과목 기말고사를 망쳐서 기분이 좋지 않다. 서훈이는 스트레스도 풀 겸 시험 문제로 나온 그래프를 불로 태우려고 한다.
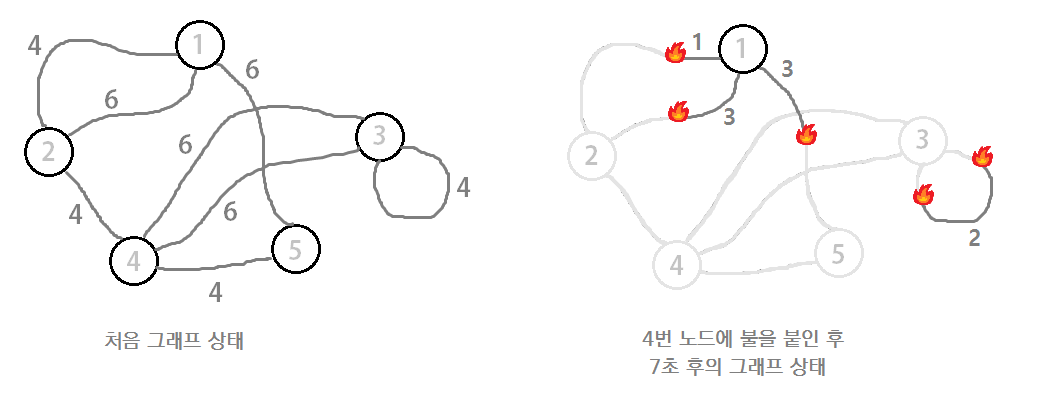
서훈이는 그래프의 정점 (위 그림에서 동그라미로 표시된 곳) 중 한 곳에 불을 붙일 수 있다. 정점에 불이 붙으면 곧바로 노드와 연결된 간선을 따라서 불이 전달된다. 간선 위에서는 불은 1초당 1만큼의 거리를 이동한다. 만약 어떤 간선의 양 끝 정점에 불이 붙은 경우 불은 간선의 중앙까지 태운 후 꺼진다.
서훈이는 그래프를 최대한 빠른 시간 안에 전부 태우고 싶어한다. 서훈이를 도와 어떤 정점에 불을 붙일지 구하는 프로그램을 작성하여라. 단, 위 그림에서 간선끼리 교차하는 것은 무시한다.
입력
첫 번째 줄에는 그래프의 정점의 수 N과 간선의 수 M이 주어진다. (2 ≤ N ≤ 200, N-1 ≤ M ≤ 20,000)
두 번째 줄부터 M개의 줄에는 각 간선의 시작점 S, 끝점 E, 길이 L이 주어진다. (1 ≤ L ≤ 100)
시작점과 끝점이 같은 간선도 있을 수 있으며, 특정 두 정점을 직접 연결하는 간선의 수가 여러 개일 수 있다. 또한, 그래프의 모든 정점들은 간선들을 통해서 연결되어 있다.
출력
주어진 그래프를 모두 태우는 데 걸리는 최소 시간을 출력한다. 답은 소수점 아래 한 자리까지 출력한다. 문제의 특성 상 오차가 생길 일이 없으므로 출력 데이터와 정확히 일치해야 정답으로 처리한다.
예제 입력 1 복사
5 8
1 2 4
1 2 6
1 5 6
2 4 4
4 5 4
3 4 6
3 4 6
3 3 4
예제 출력 1 복사
9.0
예제 입력 2 복사
5 10
1 2 1
2 3 1
3 4 1
4 5 1
1 3 10
2 4 10
3 5 10
1 4 7
2 5 7
1 5 9
예제 출력 2 복사
6.5
힌트
예제 2 설명 : 3번 정점에 불을 붙여야 그래프가 가장 빨리 모두 태워진다.
코드 풀이 참고
https://everenew.tistory.com/169
[백준] No.13141 - Ignition (C++, 플로이드-와샬)
문제 https://www.acmicpc.net/problem/13141 13141번: Ignition 첫 번째 줄에는 그래프의 정점의 수 N과 간선의 수 M이 주어진다. (2 ≤ N ≤ 200, N-1 ≤ M ≤ 20,000) 두 번째 줄부터 M개의 줄에는 각 간선의 시작점 S,
everenew.tistory.com
플로이드 워셜 알고리즘에 대한 이해도가 충분해야 풀 수 있을듯한 플레티넘5 문제였다. 풀이 방안을 떠올리기 어려웠지만 막상 풀이 방법을 알고나면 꽤 이해가 쉬웠던 문제이기도 하다.
1. 입력을 모두 받아준다.
2. 가장 작은 거리를 담은 벡터 그래프를 생성해준다.
3. 가장 먼 거리를 담은 벡터 그래프를 생성해준다.
4. 플로이드 워셜 알고리즘을 돌려서 최단거리를 각각 갱신해 준다.
5. 브루트 포스를 활용하여서 start 정점에서 모든 from to를 방문하고 그 중에서 가장 오래 걸리는 시간의 최솟값을 구해준다.
- 여기서 특이한 점은 연결된 노드의 거리 중 edge_len을 가장 거리가 먼 간선이라고 하였을 때 가장 거리가 짧은 간선의 거리가 불이 붙어 다 타게 된다면 양쪽에서 불이 붙기 때문에 2배 빨리 타게 된다. 그래서 이것을 구하기 위해서 가장 긴 거리를 담은 벡터와 가장 작은 거리를 담은 벡터를 이용해준것이다. 따라서 남은 거리는 remain_len = edge_len - dist[start][to] - dist[start][from] 이고 만약 remain_len이 0보다 작다면 모두 탄 것이고 크다면 아직 덜 탄 것이다. 만약 덜 탔다면 아까 말했듯이 2배로 빨리 타기 때문에 연결된 모든 간선이 총 타들어가는 시간은 remain_len/2 + dist[start][to]가 된다. 그래서 이렇게 구한 시간들중에 가장 최솟값을 계속해서 갱신 시키고 출력하게 되면 그게 정답이 된다. 왜냐하면 브루트포스를 통해서 모든 start to start form을 방문하면서 가장 작은 값을 찾은 것이기 때문이다.
- c++ 풀이
#include <bits/stdc++.h>
using namespace std;
const int INF = 987654321;
int vertex_num, edge_num;
vector<vector<int>> adj; //실제 간선으로 이어진 경우만 저장
vector<vector<int>> dist; //플로이드로 계산한 최단 경로를 저장
double BurnGraph() {
double shortest_time = INF, longest_time, spent_time, remain_len;
int edge_len;
for (int start = 1; start <= vertex_num; ++start) {
//start 정점부터 태웠을 때 마지막 간선이 사라지는 시간을 저장
longest_time = 0;
for (int from = 1; from <= vertex_num; ++from) {
for (int to = 1; to <= vertex_num; ++to) {
edge_len = adj[from][to];
if (edge_len != -1) { //from 정점과 간선으로 연결되지 않은 경우
remain_len = edge_len - (dist[start][to] - dist[start][from]);
//remain_len이 0이하이면 이미 불탄 경우를 의미
if (remain_len > 0) {
spent_time = (remain_len / 2) + dist[start][to];
longest_time = max(spent_time, longest_time);
}
}
}
}
//어떤 정점부터 태워야 가장 빨리 모든 그래프를 태울 수 있는지 저장
shortest_time = min(longest_time, shortest_time);
}
return shortest_time;
}
void Floyd() {
for (int k = 1; k <= vertex_num; ++k)
for (int i = 1; i <= vertex_num; ++i)
for (int j = 1; j <= vertex_num; ++j)
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
int main() {
scanf("%d %d", &vertex_num, &edge_num);
adj = vector<vector<int>>(vertex_num + 1, vector<int>(vertex_num + 1, -1));
dist = vector<vector<int>>(vertex_num + 1, vector<int>(vertex_num + 1, INF));
for (int i = 1; i <= vertex_num; ++i)
dist[i][i] = 0;
int S, E, L;
for (int i = 0; i < edge_num; ++i) {
scanf("%d %d %d", &S, &E, &L);
if (adj[S][E] == -1 || adj[S][E] < L) {
adj[S][E] = L;
adj[E][S] = L;
}
if (dist[S][E] == INF || L < dist[S][E]) {
dist[S][E] = L;
dist[E][S] = L;
}
}
Floyd();
printf("%.1f\n", BurnGraph());
return 0;
}
'Algorythms' 카테고리의 다른 글
| 백준 11557번 Yangjojang of The Year c++ 풀이 (1) | 2023.11.25 |
|---|---|
| 백준 14936번 서강그라운드 c++ 풀이 (0) | 2023.11.24 |
| 백준 1389번 케빈 베이커의 6단계 법칙 풀이 java (2) | 2023.11.22 |
| 백준 2458번 키 순서 java 풀이 (0) | 2023.11.21 |
| 백준 11404번 플로이드 java 풀이 (1) | 2023.11.20 |



